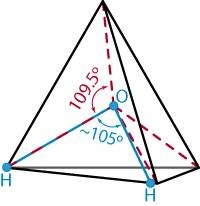
Regarding "Simulating Water and the Molecules of Life," by Mark Gerstein and Michael Levitt [November 1998]: the authors write that "the angle formed between the two sides of the V [of a tetrahedron] is close to 105 degrees--slightly less than the 109.5-degree angle formed between any two sides of a perfect tetrahedron." Any two triangular, planar sides of a perfect tetrahedron meet to form an angle of just over 70 degrees. The V formed by two radii connecting the geometric center of a regular tetrahedron with two of its vertices has an angle of 109.5 degrees. These radii represent the bonds formed between an oxygen nucleus and hydrogen nuclei in a water molecule; these bonds do form an angle of 105 degrees, as mentioned previously.
JOHN W. JOHNSON
Santa Barbara, Calif.
Gerstein and Levitt reply:
Johnson is correct that the way we described the geometry
of a water molecule was somewhat imprecise. The exact details
of this geometry and its relation to the tetrahedron are best
expressed not in words but pictorially, as shown at the right.
The bonds in the water molecule correspond to the radii rather
than to the sides of the tetrahedron.

Additional picture showing tetrahedral geometry in more detail.